Het verborgen PAD

Achtergrondinformatie zie: "Zeven Invalshoeken voor Vakdidactiek"

Samenvatting
In de blog over Goed lezen bestaat uit drie onderdelen is uiteengezet dat de meeste bedrijfseconomische vraagstukken vanuit de wiskunde gezien een functievoorschrift missen. Er zijn een of meer onbekenden die opgelost moeten worden met twee of meer gegevens. Hoe die gegevens gecombineerd moeten worden, staat er niet bij, want dan wordt het vraagstuk te makkelijk. Daarom moeten de leerlingen zelf het PAD bedenken dat vanaf de gegevens leidt naar de uitkomst van de gevraagde grootheden.

Voorbeeld 3.c bij blog nummer 3
Expliciteren van het instructieproces tijdens het onderwijs"

Het verborgen PAD

In de blog over Goed lezen bestaat uit drie onderdelen is een schema gebruikt om duidelijk te maken hoe de samenhang is tussen de gegevens en de gevraagde grootheid in een economische opgave. Ook is te zien welke tussenstappen nodig zijn om de gevraagde berekening uit te voeren. Deze manier van schematiseren is bij veel (bedrijfs)economische vraagstukken mogelijk. Zij geeft ook direct een beeld van de fundamentele vraagstukken en de wendbaarheidsvraagstukken die opduiken in de economische leerboeken.


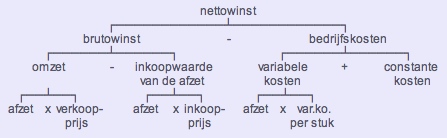
 Het PAD voor de berekening van de nettowinst bij bedrijfseconomie

Fundamentele vraagstukken
Het fundamentele vraagstuk dat bij dit PAD hoort, is gericht op de grootheid die aan de top van dit schema staat. Het gaat in feite om problemen waar een ondernemer mee in aanrakning komt. Eigenlijk sluit daarop een vraag aan die de ondernemer vanuit zijn bedrijfsvoering kan stellen: "Welke gegevens heb ik nodig om hier antwoord op te krijgen?". In leerboeken staan die gegevens al opgesomd, omdat de schrijver van het boek niet bij machte is om later gegevens toe te voegen.

Bijvoorbeeld:
Een ondernemer wil zijn winst berekenen en heeft de volgende data verzameld: de verkoopprijs is € 80,- per stuk, terwijl de inkoopprijs € 50,- per stuk is, de afzet is 400 stuks per maand, de constante kosten zijn € 5000,- per maand en aan variabele kosten komt daar nog € 10,- per verkochte eenheid bij.
Gevraagd: hoe groot is de nettowinst?

Het oplossingspad bestaat uit de volgende 6 handelingsvoorschriften:
* omzet = afzet x verkoopprijs
* inkoopwaarde afzet = afzet x inkoopprijs
* brutowinst = omzet - inkoopwaarde van de afzet
* variabele kosten = afzet x variabele kosten per stuk
* bedrijfskosten = variabele kosten + constante kosten
* nettowinst = brutowinst - bedrijfskosten.

Variaties op een fundamenteel vraagstuk
Op dit vraagstuk zijn allerlei variaties mogelijk. De auteur van een boek kan het vraagstuk verkorten door direct al de waarde van de omzet en de inkoopwaarde van de omzet te geven. Of hij kan het verlengen door de constante kosten en/of de variabele kosten uit te splitsen in inkoopkosten, algemene kosten en verkoopkosten. Hoe verder de uitsplitsing gaat, hoe moeilijker het vraagstuk wordt.

Ook is het mogelijk om de moeilijkheidsgraad van het vraagstuk in te perken door te vragen naar de waarde van de tussenstappen. In plaats van de vraag hoe groot de nettowinst is, kan hij de vraag opslitsen, bijvoorbeeld:
a. hoe groot is de brutowinst?
b. hoe groot zijn de bedrijfskosten?
c. hoe groot is de nettowinst?

In al deze variaties op het fundamentele vraagstuk blijft het pad dat leidt van de gegevens naar de onbekende grootheid verborgen. Om dat te vinden, moet de leerling zich uit een voorbeeld herinneren hoe dit pad luidt, of zelf bedenken wat een logische samenhang is, of gokken. In een aparte blog is aangegeven hoe ver een leerling kan komen met gokken.

Wendbaarheidsvraagstukken
Op basis van bovenstaand PAD is het ook mogelijk om een tweede type vraagstukken te maken. Het gaat dan om de wendbaarheid van kennis door de oorspronkelijke onbekende grootheid (de centrale grootheid) van een waarde te voorzien. Vervolgens kan men een van de oorspronkelijke gegevens tot onbekende grootheid verheffen.

Bijvoorbeeld, Welke verkoopprijs is nodig om een nettowinst van € 3000,- per maand te behalen?

In die situatie is het schema, c.q. het Probleem Analyse Diagram, oftewel het pad, hetzelfde. Alleen het oploissingspad verandert. De volgorde van de bewerkingen wordt anders. En de berekeningen lopen soms in toegenovergestelde richting, waarbij de wiskundig bewerking omkeert. Aftrekken wordt optellen en vermenigvuldigen wordt delen.

Het oplossingspad bij de vraag naar een gewenste verkoopprijs bestaat nu uit de volgende 6 handelingsvoorschriften:
* variabele kosten = afzet x variabele kosten per stuk
* bedrijfskosten = variabele kosten + constante kosten
* inkoopwaarde afzet = afzet x inkoopprijs
En dan komen de omgekeerde bewerkingen:
* brutowinst = nettowinst + bedrijfskosten
* omzet = brutowinst + inkoopwaarde van de afzet
* verkoopprijs = omzet / afzet.

Dus niet alleen de volgorde binnen een handelingsvoorschrift verandert, maar ook de wiskundige bewerking. Min wordt plus: brutowinst = nettowinst + bedrijfskosten. En een vermenigvuldiging wordt een deling: verkoopprijs = omzet / afzet. Dit maakt wendbaarheidsvraagstukken moeilijker dan fundamentele vraagstukken. Nu doorloopt de leerling het PAD op een hele andere manier dan bottom up, zoals bij fundamentele vraagstukken.

Variaties op wendbaarheidsvraagstukken
in principe is het mogelijk om uit een fundamenteel vraagstuk net zoveel wendbaarheidsvraagstukken te halen als er gegevens zijn. Elke oorspronkelijk gegeven kan tot onbekende grootheid verheven worden, door aan alle andere gegevens een waarde toe te kennen en ook aan de oorspronkelijke, centrale, grootheid. Bovendien kan het oorspronkelijke fundamentele vraagstuk verlengd worden, waardoor extra gegevens en dus extra onbekenden toegevoegd kunnen worden.

Een van de bekendste wendbaarheidsvraagstukken bij dit PAD is de vraag bij welke afzet de nettowinst precies gelijk is aan € 0. Dit heet de de break-even-analyse. De oplossing is te standaardiseren door het PAD samen te vatten in een formule. De tussenresultaten, zoals bedrijfskosten, nettowinst en brutowinst blijven buiten de berekening. Dat kan door de samenhang rechtstreeks te formuleren:

* omzet - inkoopwaarde omzet = variabele kosten + constante kosten, dus
* omzet = inkoopwaarde omzet + variabele kosten + constante kosten, dus
* constante kosten = omzet - inkoopwaarde omzet - variabele kosten, dus
* constante kosten = afzet x (verkoopprijs - inkoopprijs - var. kosten per stuk)

Uit die tussenstappen vloeit een formule voort:
De (break-even) afzet = constante kosten / (verkoopprijs - inkoopprijs - variabele kosten per stuk).

Micro-economische variant
In de micro economie is dat nog iets eenvoudiger geformuleerd:
b.e.afzet = c / (p - v).

Maar daar passen ze een truc toe door de inkoopprijs als variabele kosten te laten gelden. Dat betekent dat de micro-economie geen weet heeft van de term brutowinst. Bovendien omschrijven zij de begrippen anders, zoals te zien is in het PAD dat gebruikelijk is om de winst te berekenen. Hieruit volgt dat de variatie in het PAD niet alleen te vinden is in de lengte van het pad en de getallen die in gebruik zijn, maar ook in de naamgeving van de grootheden waarmee men werkt.

Het PAD voor de berekening van de totale winst bij micro-economie

Computermogelijkheden voor een PAD
Een computer is een ander leermiddel met een andere didactiek. Een computer kan gegevens achterhouden alsmede vragen over de tussenresultaten. Pas als een leerling of student vastloopt in de beantwoording van vragen kan de computer ingrijpen.

Via het beeldscherm is dan de vraag te stellen "Welke gegevens heeft een ondernemer nodig om de nettowinst te berekenen?." Of: "... om de kostprijs te berekenen van een houten kast?". Ook de vragen naar de tussenresultaten kunnen buiten beeld blijven tot de leerling aangeeft dat hij of zij niet verder kan.

Eigenlijk is de explicitering van het verband tussen gegevens en onbekende grootheid in een PAD het gevolg van de ontwikkeling van computer ondersteund onderwijs. Om een consistente communicatie met de studenten op te zetten, is de systematiek ontwikkeld om bedrijfseconomische begrippen in schema te plaatsen. Vervolgens zijn de schema's gebruikt om te tonen als achtergrondinformatie bij de uitwerking van vraagstukken. De resultaten van dit onderzoek zijn te vinden op de website "Bedrijfseconomische modellen".

Verdere uitwerking
Een volledige analyse van het voorbeeld dat hier boven staat, is te vinden in de website: "Vakdidactiek Bedrijfseconomie".

Alle blogs over de zeven invalshoeken van vakdidactiek
In totaal zijn de volgende blogs verschenen, waarin de zeven invalshoeken voor vakdidactiek successievelijk terugkomen. Bij een aantal blogs zijn een of meer voorbeelden toegevoegd. Daarnaast is er een blog met achtergrond informatie over de zeven invalshoeken waarin onderdelen nader uitgewerkt of toegelicht staan om veelvuldige herhaling te voorkomen.

De zeven invalshoeken voor vakdidactiek (achtergrondinformatie):

1. Becommentariëren en verbeteren van bestaande lesprogramma;
2. Beschrijven van de mentale voorstelling die docenten hebben
   van hun vak;
   - Voorbeeld 2.a De namen van leerlingen leren;
    
3. Expliciteren van het instructieproces tijdens het onderwijs;
   - Voorbeeld 3.a De vele talen van de wiskunde;
   - Voorbeeld 3.b Goed lezen bestaat uit drie onderdelen;
   - Voorbeeld 3.c Het verborgen pad;
   - Voorbeeld 3.d Het gebruik van eenheden;
   - Voorbeeld 3.e Verpleegkundig rekenen bijvoorbeeld;
    
4. Stimuleren van de motivering van leerlingen door de vorm
   van het lesaanbod;
5. Bevorderen van de zelfsturing van leerlingen door eigen
   organisatie van het onderwijs;
6. Analyseren van de problemen die leerlingen hebben met de stof;
   - Voorbeeld 6.a Rekenen met procenten;
    
7. Onderzoeken welke mentale modellen leerlingen ontwikkelen
   en toepassen;
   - Voorbeeld 7.a Onderzoek via hardop-denk-sessies;
   - Voorbeeld 7.b Op zoek naar gokstrategieën.
   - Voorbeeld 7.c Wanneer ken je een hoofdstuk?

Bronnen
- Norman, D.A., Gentner, D.R. & Stevens, A.L. (1976), Comments on
  learning schemata and memory representation. In D. Klahr (ed.),
  Cognition and Instruction, Hillsdale N.J. Lawrence Erlbaum Ass.
- Kneppers, L., Zelfstandig leren leren, Factor D, 2011, nummer 4.
- Van Dongen, H. en Van der Meche, E., Mentale Modellen, Factor D, 2022,
  nummer 1, blz 13.
- Vernooij F., "Zelfstandig leren lezen". Factor D, 2012, nummer 2, blz 4.
  nummer 2, blz.17.
- Vernooij, F., Een mentaal model van vakdidactiek. Factor D, 2022,
  nummer 2, blz.17.
- Vernooij, F., Bedrijfseconomische begrippen en hun eenheden.
  Zie: bedrijfseconomische-begrippen.nl.

Persoonsgegevens
Fons Vernooij was Vakdidacticus bedrijfseconomie en algemene economie bij het ILO in Amsterdam en is nu met pensioen. Hij beheert de website vakdidactiek.nl als onderdeel van zijn website onderwijsportaal.nl. Vanwege zijn achtergrond zijn veel voorbeelden ontleend aan de economische vakken.

Als vakdidacticus voerde hij in 1993 een promotieonderzoek uit. Zie: Vernooij, F., (1993), Het leren oplossen van bedrijfseconomische problemen. Proefschrift, te vinden op vakdidactiek-bedrijfseconomie.nl.

Deze blogs zijn een uitvloeisel van zijn artikel “Een mentaal model van vakdidactiek”, dat is verschenen in het blad Factor D (didactiek), veertigste jaargang, nummer 2 uit 2022. Dit artikel is te downloaden via www.fons-vernooij.nl/documenten/een-mentaal-model-van-vakdidactiek.pdf.